ramasubramanian.github.io
Blog
Constraint Programming
We as developers have always been programming with constraints like deadlines, changing user requirements, internet downloading build systems, FP vs OOP dilemma, to use or not to use the new shiny web framework of the week, half assed tech bros, slow compiling languages, meetings etc. But this post is not about developer constraints.
This is about programs which run based on specific constraints and try to find out solutions for us based on the constraints i.e. rules. It is a different programming paradigm.
Programming is always about finding solutions at various degrees of scale. A software platform finds solution to an existing business problem as a whole. Components of the software system finds solutions to parts of the business problem. Individual class/code running within those components find solutions to their respective problems at a granular level. If your problem composes then the solution also composes.
Some (or most) problems might be as good as finding applicable values for variables based on a set of rules. Constraint programming enables us to specify these rules as models and allow the system to find appropriate values for the variables.
Wannabe mathematician impostor alert below!!!
Suppose there are two variables V1, V2, ..., Vn which can have possible values from domain D1, D2,..., Dn respectively and the relationships between those variables are specified as a set of rules aka Constraints C1, C2, ..., Cm where m > 0 and m = n or m <> n then a program P which finds the appropriate values of V1, V2, ..., Vn from respective domains which satisfy the constraints is called a constraint programming system. At the end of successful execution we will have V1=d1, V2=d2, ..., Vn=dn where d1, d2,..., dn are specific values from domains D1, D2,..., Dn respectively.
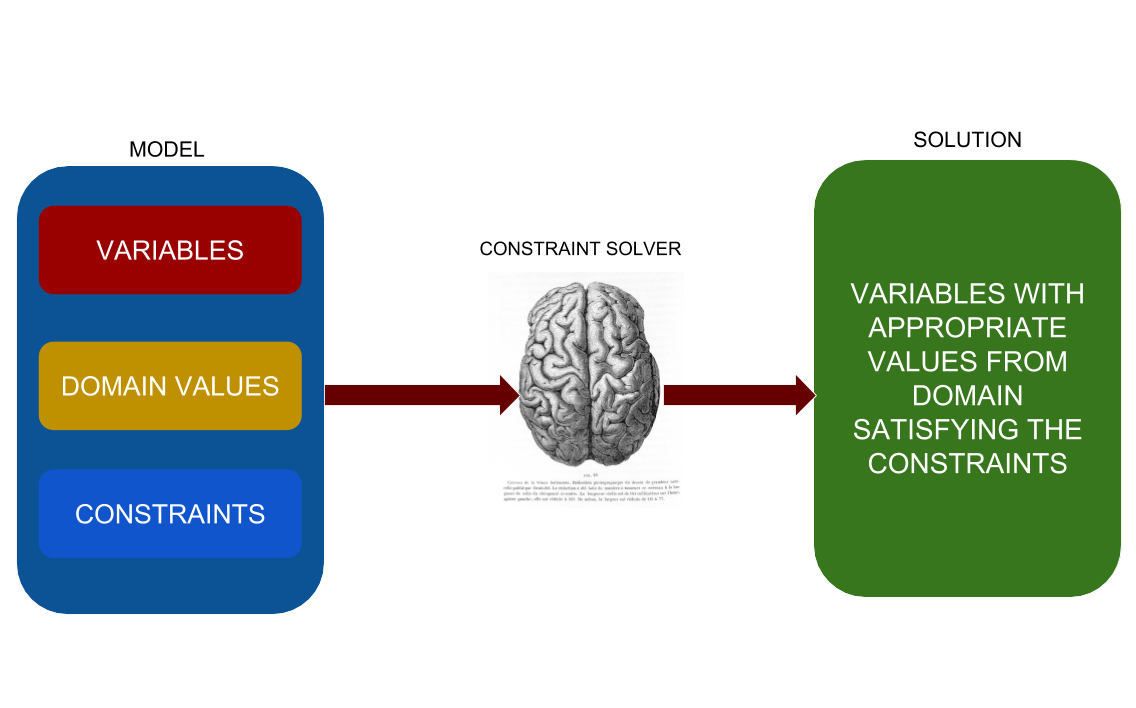
So is the system intelligent enough to find a solution?

NOOOOOOO!
Now the variables can be of type simple integers to arrays/sets or matrices. Each corresponding value domain will obviously be of the same data type as the variable.
Current state and library choices
Our industry is driven by libraries created by computer science literates turned developers and normal developers who understand (rarely ;-)) then use those libraries to create wonderful products. Similar to any CS concept there are a good number of open source constraint programming libraries available in the market. We initially evaluated multiple choices and landed up on Google Optimisation tools, of course standing in the shoulder of a giant is safe isn’t it?
The library has multiple(awesome) functionality and necessary wrappers in java, python and .net, however we tried using the java wrappers as the customer was a java shop. Though the documentation was vague and we have to scan through reference docs we were able to write some programs and spike it out. Even though the wrappers were in java the core has been written in C++ and any exception stack traces ended up us reading C++ code to figure out the problem. This was confusing with minimal help from documentation (we did this 1.5 years ago, may be the docs are good now).
After facing some road blocks with Google’s implementation I set out to find alternative library choices and ended up with Choco Solver. This is a sweet (pun intended), pure java library for Constraint Programming. The DSL they have used was easy, stack traces were traceable to Java code and was relatively easier for us to use. The pleasure of adding it just like Google Guava or another utility in our build gradle file was good. The creators are also pretty responsive in support forums for queries.
A Simple example or how to draw an owl or Hello World!
Let us consider our simple school math equation problem.
Given
a + b = 8
a - b = 4
find the value of a and b
Our typical approach to solve this problem using a paper and pen would be:
1. a = 4 + b
2. a + b = 8
3. (4 + b) + b = 8
4. 4 + 2b = 8
5. 2b = 8 - 4
6. 2b = 4
7. b = 4 / 2
8. b = 2
9. a + b = 8
10. a + 2 = 8
11. a = 8 - 2
12. a = 6
13. a = 6, b = 2
Choco Solver basics
In Choco solver (v4) the whole problem is abstracted as a Model object which contains all the variables, constraints along with applicable value domains for variables. So first we have to create a model.
Model model = new Model("Simple Problem");
Now after having created a model we need to start defining the variables for which we need the values from the solver.
IntVar a = model.intVar("a", 1, 8);
IntVar b = model.intVar("b", 1, 8);
a is an integer variable with name “a” (of course!) and applicable values ranging from 1 to 8 which is the applicable domain of this variable.
Since our constraint is a + b = 8 and a - b = 4 a or b cannot be greater than 8. So we restrict the domain from 1 to 8 for logical reason and simplicity purposes.
Next step will be to specify the constraints. Choco solver has a nice DSLesque way to specify simple arithmetic constraints.
//a + b = 8
model.arithm(a, "+", b, "=", 8).post();
//a - b = 4
model.arithm(a, "-", b, "=", 4).post();
Note: Always remember to call .post() after declaring each constraint else choco solver will forget it
Now each model will have a corresponding Solver implementation which does the heavy work of finding suitable solutions from the search space. Solver has a solve() method which will return us true/false depending on whether a solution is found or not. If the solution is found then the variables i.e. IntVar we declared earlier will have the values corresponding to the current solution.
To extract all possible solutions we can use code below:
package com.ajira.chocosolver;
import org.chocosolver.solver.Model;
import org.chocosolver.solver.variables.IntVar;
public class SimpleConstraint {
public static void main(String[] args) {
Model model = new Model("Simple Constraint");
IntVar a = model.intVar("a", 1, 8);
IntVar b = model.intVar("b", 1, 8);
//a + b = 8
model.arithm(a, "+", b, "=", 8).post();
//a - b = 4
model.arithm(a, "-", b, "=", 4).post();
int i = 1;
while (model.getSolver().solve()) {
System.out.println("Solution " + (i++) + " found : " + a.getValue() + ", " + b.getValue());
}
}
}
Notice the a.getValue() calls to extract the value of a variable for the current solution. Wish i knew this in school for those math equation assignments ;-)
This is a simple problem with a very small search space i.e. 2 variables with 8 applicable values each. Real life problems are more complex and can have millions of combinations to search for. That is were an optimisation problem kicks in and specific solvers take care of the finding the best solutions.
Output of the above program would be:
Solution 1 found : 6, 2
Which is the same as our paper and pencil solution. We took some few seconds or a minute but the system responds immediately!
If you want to find solutions for equations like
2a + 3b = 16
2a - b = 2
The same can be done using below code specifying the constraints
IntVar c = model.intScaleView(a, 2); //(2 * a)
IntVar d = model.intScaleView(b, 3); //(3 * b)
model.arithm(c, "+", d, "=", 16).post(); //2a + 3b = 16
model.arithm(c, "-", b, "=", 2).post(); //2a - b = 2
Now that we have understood how to draw an Owl via simple steps (image on the left), let us draw an actual owl (image on the right)

Image credits: https://eurokeks.com/memes/how-to-draw-an-owl
Drawing an actual Owl or using CP to solve an actual problem
So in our customer place we had a problem of scheduling a set of tasks for a set of employees. No I am not going to discuss the schedule generation part even though that was solved using CP. Even before scheduling we have to group these tasks into N minute sessions of fixed time so that it can be evenly distributed among employees. Since each task can take variable times with a high degree of variations like 1 minute task to 15 minute task choosing the best combination of tasks for grouping into 1 hour sessions so that number of sessions are kept minimal and hence the breaks between each sessions is minimal was a challenge. There can be 1000s of tasks per day distributed across 100s of employees. Using naive approach or writing a custom algorithm does not work since the search space is huge.
So in essence it is grouping n tasks T1, T2,..., Tn into m sessions S1, S2, ..., Sm where m <= n so that m is minimal. There is no restriction on the number of tasks a session can hold. The expected output for example is
S1 = {T23, T28, T89}
S2 = {T1, T7}
S3 = {T90}
.
.
.
Sm = {Tn-1, Tn}
You can notice that each session here can be considered as bin inside which each task is an object of a specific volume i.e. time taken to complete that task. So this is apparently a form of bin packing optimisation problem which is common in Constraing Programming domain. Thankfully our CS literates have exposed APIs in Choco Solver to find solutions for such bin packing problems.
We will follow an approach similar to the simple equation problem, first let us define the required data models and variables
Defining the data models
static class Task {
public final String taskName;
public final Integer durationMinutes;
public final Integer id;
public Integer sessionIndex;
public Task(String taskName, Integer durationMinutes, Integer id) {
this.taskName = taskName;
this.durationMinutes = durationMinutes;
this.id = id;
}
@Override
public String toString() {
final StringBuffer sb = new StringBuffer("Task{");
sb.append("taskName='").append(taskName).append('\'');
sb.append(", durationMinutes=").append(durationMinutes);
sb.append(", id=").append(id);
sb.append(", sessionIndex=").append(sessionIndex);
sb.append('}');
return sb.toString();
}
}
The above class represents the data model of a basic task which can have an unique name, a unique ID and duration i.e. estimated time of the task taken in minutes
Now let us write a utility method to generate tasks in memory, ideally this would come from external source like a DB or so.
private List<Task> generateTasks(int count) {
Random random = new Random(System.currentTimeMillis());
return IntStream.range(1, count + 1)
.mapToObj(i -> new Task("T" + i, random.nextInt(15) + 1, i))
.collect(Collectors.toList());
}
We generate task ids and names using indexes from 1 to 30 and we assign a random time taken for each task.
Defining the variables
Before creating necessary variables let us see the documentation of binpacking constraint method to understand the set of variables which we would require
Constraint binPacking(IntVar[] itemBin, int[] itemSize, IntVar[] binLoad, int offset)
itemBin - An array of integer variables denoting the bin number of each item which will be placed in the bin. In our case it is the variable for each task whose value would be 0 to N where N is maximum number of bins i.e. sessions
itemSize - An int array specifying the size of each item to be placed in the bin, in our case it is the estimated duration of each task
binLoad - An array of integer variables specifying the load of each bin as a range from minumum bin capacity to maximum bin capacity i.e. sessions in our case where minimum session capacity will be 0 minutes to maximum capacity will be 45 minutes
offset - Default to 0, not relevant for our use case now
Now let us define the variables for modelling our tasks.
List<Task> tasks = generateTasks(30);
int maxSessionCount = 30;
IntVar[] taskVars = tasks.stream().map(t ->
model.intVar(t.taskName, 0, maxSessionCount, false))
.toArray(IntVar[]::new);
Each variable should have a unique name so we are using the task name itself as the variable name. The range of applicable values for each task variable can be 0 to max session count which in our case would be same as number of tasks.
Next we will proceed to create the variables required for modelling our sessions
IntVar[] sessionVars = IntStream.range(0, maxSessionCount)
.mapToObj(Integer::new)
.map(i -> model.intVar("Session:" + i, minSessionTimeMinutes, maxSessionTimeMinutes, true))
.toArray(IntVar[]::new);
For each session we assign a unique name "Session:1", "Session:2" etc. until max session count. The applicable domain values are from 0 to max session time i.e. 45 minutes in our case.
Once a solution is found we need to have the handle of each task variable to find the session index to which it would belong to. So we will save each variable in a map to lookup using the task name.
Map<String, IntVar> taskVarMap = Arrays.stream(taskVars)
.collect(Collectors.toMap(Variable::getName, Function.identity()));
Specifying the constraints
Now let us move on to specifying the constraints, as we have already seen we are going to define a bin packing constraint. We will do the same as below:
model.binPacking(taskVars, tasks.stream().mapToInt(t -> t.durationMinutes).toArray(), sessionVars, 0).post();
The 3rd argument i.e. size of each item is extracted from task list. Other arguments are self explanatory.
Even though we have specified the bin-packing constraint there may be N number of possible solutions for this problem. However we are interested in that one particular solution that will enable us to have minimum number of sessions i.e. bins (yes! we always prefer the best solution if we are NOT solving the problem right?). So we will specify an additional minimisation goal for the solver.
IntVar sessionCountVar = model.intVar("sessionCount", 0, maxSessionCount);
model.max(sessionCountVar, taskVars).post();
model.setObjective(Model.MINIMIZE, sessionCountVar);
The first new variable is necessary to provide a storage to keep the maximum of sessionIndex i.e. the session count. So if we try to minimise the value of this max(session index) then we can ensure we will have minimum number of sessions and in turn less breaks between the sessions.
Now just run the solver to get necessary output.
model.setObjective(Model.MINIMIZE, sessionCountVar);
Solution solution = new Solution(model);
//set run time limit to 5 minutes for this solver
model.getSolver().limitTime(5 * 60 * 1000);
while (model.getSolver().solve()) {
solution.record();
}
boolean solved = model.getSolver().getSolutionCount() > 0;
Extracting the solutions
If solved is true then we can extract the values from variables and assign the same to corresponding tasks and group them into sessions as shown below:
if(solved) {
//for each task get the value from corresponding variable and save to task object
tasks.forEach(t -> t.sessionIndex = solution.getIntVal(taskVarMap.get(t.taskName)));
//group the tasks by session index
Map<Integer, List<Task>> grouped = tasks.stream().collect(Collectors.groupingBy(t -> t.sessionIndex));
System.out.println();
System.out.println();
this.printSessionSummary(grouped);
} else {
System.out.println("No solution found");
}
Now the complete program:
package com.ajira.chocosolver;
import org.chocosolver.solver.Model;
import org.chocosolver.solver.Solution;
import org.chocosolver.solver.variables.IntVar;
import org.chocosolver.solver.variables.Variable;
import java.util.Arrays;
import java.util.List;
import java.util.Map;
import java.util.Random;
import java.util.function.Function;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
public class Task2Sessions {
static class Task {
public final String taskName;
public final Integer durationMinutes;
public final Integer id;
public Integer sessionIndex;
public Task(String taskName, Integer durationMinutes, Integer id) {
this.taskName = taskName;
this.durationMinutes = durationMinutes;
this.id = id;
}
@Override
public String toString() {
final StringBuffer sb = new StringBuffer("Task{");
sb.append("taskName='").append(taskName).append('\'');
sb.append(", durationMinutes=").append(durationMinutes);
sb.append(", id=").append(id);
sb.append(", sessionIndex=").append(sessionIndex);
sb.append('}');
return sb.toString();
}
}
private List<Task> generateTasks(int count) {
Random random = new Random(System.currentTimeMillis());
return IntStream.range(1, count + 1)
.mapToObj(i -> new Task("T" + i, random.nextInt(15) + 1, i))
.collect(Collectors.toList());
}
private void printSessionSummary(Map<Integer, List<Task>> sessions) {
String sessionFormat = "| %-15d | %-12d | %-17d | %-65s |%n";
System.out.println("----------------------------SESSIONS--------------------------");
System.out.format("+-----------------+--------------+-------------------+--------------------------------------------------------%n");
System.out.format("| Session Index | Task Count | Duration(Minutes)| Tasks |%n");
System.out.format("+-----------------+--------------+-------------------+--------------------------------------------------------%n");
sessions.entrySet().forEach(sessionData -> {
System.out.format(sessionFormat, sessionData.getKey(), sessionData.getValue().size(),
sessionData.getValue().stream().mapToInt(t -> t.durationMinutes).sum(),
sessionData.getValue().stream().map(t -> t.taskName + '=' + t.durationMinutes)
.collect(Collectors.joining(",")));
});
System.out.format("+-----------------+--------------+-------------------+--------------------------------------------------------%n");
}
private void group2Sessions(int taskCount) {
Model model = new Model("Tasks to Sessions grouping model");
List<Task> tasks = generateTasks(30);
String taskFormat = "| %-15s | %-4d |%-18d|%n";
System.out.println("-------------------TASKS---------------------");
System.out.format("+-----------------+------+-------------------%n");
System.out.format("| Task name | ID | Duration(Minutes)|%n");
System.out.format("+-----------------+------+-------------------%n");
tasks.forEach(t -> System.out.format(taskFormat, t.taskName, t.id, t.durationMinutes));
System.out.format("+-----------------+------+-------------------%n");
int maxSessionCount = taskCount;
int minSessionTimeMinutes = 0;
int maxSessionTimeMinutes = 60;
IntVar[] taskVars = tasks.stream().map(t ->
model.intVar(t.taskName, 0, maxSessionCount, false))
.toArray(IntVar[]::new);
IntVar[] sessionVars = IntStream.range(0, maxSessionCount)
.mapToObj(Integer::new)
.map(i -> model.intVar("Session:" + i, minSessionTimeMinutes, maxSessionTimeMinutes, true))
.toArray(IntVar[]::new);
Map<String, IntVar> taskVarMap = Arrays.stream(taskVars)
.collect(Collectors.toMap(Variable::getName, Function.identity()));
IntVar sessionCountVar = model.intVar("sessionCount", 0, maxSessionCount);
model.max(sessionCountVar, taskVars).post();
model.binPacking(taskVars, tasks.stream().mapToInt(t -> t.durationMinutes).toArray(), sessionVars, 0).post();
model.setObjective(Model.MINIMIZE, sessionCountVar);
model.getSolver().limitTime(5 * 60 * 1000);
Solution solution = new Solution(model);
//set run time limit to 2 minutes for this solver
model.getSolver().limitTime(5 * 60 * 1000);
//dont find more than 500 solutions
model.getSolver().limitSolution(500);
while (model.getSolver().solve()) {
solution.record();
}
boolean solved = model.getSolver().getSolutionCount() > 0;
if(solved) {
tasks.forEach(t -> t.sessionIndex = solution.getIntVal(taskVarMap.get(t.taskName)));
Map<Integer, List<Task>> grouped = tasks.stream().collect(Collectors.groupingBy(t -> t.sessionIndex));
System.out.println();
System.out.println();
this.printSessionSummary(grouped);
} else {
System.out.println("No solution found");
}
}
public static void main(String[] args) {
new Task2Sessions().group2Sessions(30);
}
}
Program output
Running the program gives me below output:
-------------------TASKS---------------------
+-----------------+------+-------------------
| Task name | ID | Duration(Minutes)|
+-----------------+------+-------------------
| T1 | 1 |14 |
| T2 | 2 |2 |
| T3 | 3 |4 |
| T4 | 4 |2 |
| T5 | 5 |11 |
| T6 | 6 |8 |
| T7 | 7 |8 |
| T8 | 8 |9 |
| T9 | 9 |9 |
| T10 | 10 |6 |
| T11 | 11 |7 |
| T12 | 12 |2 |
| T13 | 13 |11 |
| T14 | 14 |14 |
| T15 | 15 |2 |
| T16 | 16 |13 |
| T17 | 17 |14 |
| T18 | 18 |12 |
| T19 | 19 |9 |
| T20 | 20 |6 |
| T21 | 21 |9 |
| T22 | 22 |11 |
| T23 | 23 |11 |
| T24 | 24 |1 |
| T25 | 25 |4 |
| T26 | 26 |15 |
| T27 | 27 |12 |
| T28 | 28 |4 |
| T29 | 29 |1 |
| T30 | 30 |8 |
+-----------------+------+-------------------
----------------------------SESSIONS--------------------------
+-----------------+--------------+-------------------+--------------------------------------------------------
| Session Index | Task Count | Duration(Minutes)| Tasks |
+-----------------+--------------+-------------------+--------------------------------------------------------
| 0 | 10 | 60 | T1=14,T2=2,T4=2,T11=7,T12=2,T16=13,T20=6,T21=9,T28=4,T29=1 |
| 1 | 7 | 59 | T3=4,T8=9,T9=9,T14=14,T17=14,T24=1,T30=8 |
| 2 | 6 | 60 | T5=11,T6=8,T7=8,T10=6,T26=15,T27=12 |
| 3 | 7 | 60 | T13=11,T15=2,T18=12,T19=9,T22=11,T23=11,T25=4 |
+-----------------+--------------+-------------------+--------------------------------------------------------
You can see 30 tasks are grouped into 4 sessions of ~60 minutes each. The program takes milliseconds to run. Had we tried this using a naive approach imagine the amount of time it would have taken.
Since we are generating random duration for each tasks each time the split and grouping may not be the same for each run of the program
Your build gradle entry goes like below if you need to setup choco solver:
group 'com.ajira.chocosolver'
version '1.0-SNAPSHOT'
apply plugin: 'java'
sourceCompatibility = 1.8
repositories {
mavenCentral()
}
dependencies {
compile group: 'org.choco-solver', name: 'choco-solver', version: '4.0.1'
testCompile group: 'junit', name: 'junit', version: '4.11'
}
If you have come until this I guess you would have some questions in the mind, a mini WTFAQ given below:
What if there is no possible solution at all?
There may be edge cases or input data for which the solver might never be able to find a solution. For example conflicting constraints etc. In that case we need to look into remodelling the problem (so easy right?). Another aternative is to tweak the domain values applicable to variables if the business domain allows the same. For example let us say we reduce session time to 30 minutes and there is no good solution to fit all the tasks within, in such cases we can try ramping up the session time by a % e.g. 5% increase to 31.5 minutes instead of 30 minutes and try again.
What if the solver is running for eternity?
There may also be changes the solver will keep searching for solutions and never return due to poorly specified constraints etc. In such cases we can set a limit on how much time a solver can keep searching using the below statement:
model.getSolver().limitTime(5 * 60 * 1000);
In the above statement we set the timeout to 5 minutes for the solver. The code will return with no solution found after 5 minutes.
How to debug this?
You can use a standard CP (Constraint Programming) profiler like CP Profiler to trace and visualise how the solver works.
Parting words…
What we have seen is the tip of a tip of an iceberg. Refer the official choco documentation for more information on what this wonderful paradigm is and what the library can do to solve complex problems. Our sample problem Bin Packing can be treated as a multiple Knapsack problem. Most CP libraries have inbuilt solvers for standard problems like Knapsack, N-Queens etc.
Another wonderful source of examples using choco solver is Choco solver samples project
Even if you are not using Google’s OR library the documentation has some good information on the type of problems solved by Constraint Programming
Thanks for reading till the end, if you find any errors that needs to be corrected please drop an email to r a m [dot] 6 3 8 3 [at] g m a i l [dot] c o m